Zilverling

prof.dr. H.J. Zwart (Hans)

Professor in Physical Systems and Control/Chair Mathematics of Systems Theory
EEMCS-AM-MAST
Zilverling 3042
h.j.zwart@utwente.nl
+31534893464
Business card

Hans Zwart is Professor in Physical Systems and Control, and head of the Chair Mathematics of Systems Theory in the Department of Applied Mathematics at the University of Twente.

His research interests are in control and analysis of systems described by partial differential equation and/or time difference differential equations. The main focus is on the development and analysis of controllers for linear systems. Hereby using the mathematical techniques from functional analysis and Hamiltonian dynamics. Main area of applications is the controller design and analysis of flexible structures. On this topic he has a long lasting collaboration with research groups in Besançon, Lyon, Wuppertal, and Eindhoven. At Eindhoven University of Technology, department of Mechanical Engineering, he holds a one-day-per-week professorship. Prof. H. Zwart is the co-author of two standard text books in his field; An Introduction to Infinite-Dimensional Systems Theory, (with R. Curtain) and Linear Port-Hamiltonian Systems on Infinite-Dimensional Spaces (with B. Jacob). In 2020, an updated version of the first book has appeared. 

Organisations

Ancillary activities

  • TU/eDoing research and supervising students

Publications

Jump to: 2025 | 2024

2025

On BIBO stability of infinite-dimensional systems (2025)[Thesis › PhD Thesis - Research UT, graduation UT]. Wierzba, A. A.Port-Hamiltonian discontinuous Galerkin finite element methods (2025)IMA Journal of Numerical Analysis, 45(1), 354–403. Kumar, N., van der Vegt, J. J. W. & Zwart, H. J.https://doi.org/10.1093/imanum/drae008

2024

Port-Hamiltonian Discontinuous Galerkin Finite Element Methods (2024)[Thesis › PhD Thesis - Research UT, graduation UT]. University of Twente. Kumar, N.https://doi.org/10.3990/1.9789036563918MATLAB files underlying the manuscript: Symplectic Model Order Reduction of port-Hamiltonian Systems (2024)[Dataset Types › Dataset]. 4TU.Centre for Research Data. Zwart, H.https://doi.org/10.4121/1404db4b-ffce-4a3e-84e5-eb6be6f079f9Stability via closure relations with applications to dissipative and port-Hamiltonian systems (2024)Journal of evolution equations, 24(3). Article 62. Glück, J., Jacob, B., Meyer, A., Wyss, C. & Zwart, H.https://doi.org/10.1007/s00028-024-00992-5Abstract Dissipative Hamiltonian Differential-Algebraic Equations Are Everywhere (2024)DAE Panel, 2. Zwart, H. & Mehrmann, V.https://doi.org/10.52825/dae-p.v2i.957Asymptotic Stability of Port-Hamiltonian Systems (2024)In Systems Theory and PDEs: Open Problems, Recent Results, and New Directions (pp. 91-122) (Trends in Mathematics; Vol. Part F3446). Springer. Waurick, M. & Zwart, H.https://doi.org/10.1007/978-3-031-64991-2_4Port-Hamiltonian systems and their discontinuous Galerkin discretization (2024)[Thesis › PhD Thesis - Research UT, graduation UT]. University of Twente. Cheng, X.https://doi.org/10.3990/1.9789036561273A flexible numerical tool for large dynamic DC networks (2024)[Working paper › Preprint]. ArXiv.org. Luesink, E., Giraldo, J., Geurts, B., Hurink, J. & Zwart, H.https://doi.org/10.48550/arXiv.2405.20704Port-Hamiltonian formulations of the incompressible Euler equations with a free surface (2024)Journal of geometry and physics, 197. Article 105097. Cheng, X., van der Vegt, J. J. W., Xu, Y. & Zwart, H.https://doi.org/10.1016/j.geomphys.2023.105097On BIBO stability of infinite-dimensional linear state-space systems (2024)SIAM journal on control and optimization, 62(1), 22-41. Schwenninger, F. L., Wierzba, A. A. & Zwart, H.https://doi.org/10.1137/23M1563098Spectral Analysis of a Class of Linear Hyperbolic Partial Differential Equations (2024)IEEE Control Systems Letters, 8, 766-771. Hastir, A., Jacob, B. & Zwart, H.https://doi.org/10.1109/LCSYS.2024.3403472

Other contributions

Since I like to construct counter examples. I list here some of the counter examples found.

  • T+B is never invertible for suciently small B; pdf-file
  • If A generates an exponentially stable contraction semigroup, and Q is dissipative, then A+Q need not to generate a exponentially stable semigroup; pdf-file
  • A boundedly invertible and Q bounded, does not imply that AQ is densely defined; pdf-file

Research profiles

Affiliated study programs

Courses academic year 2025/2026

Courses in the current academic year are added at the moment they are finalised in the Osiris system. Therefore it is possible that the list is not yet complete for the whole academic year.

Courses academic year 2024/2025

Courses academic year 2023/2024

Although I am working on many projects, I will only mention a few of my general research projects.

Current projects

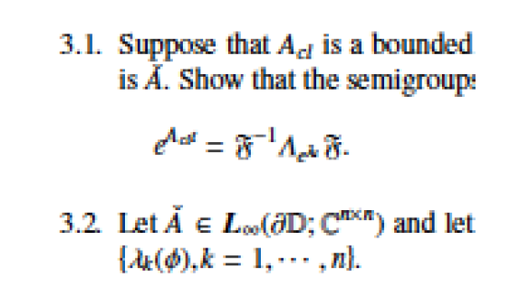
Solutions to ``Introduction to Infinite-Dimensional Systems Theory''

The two books written together with Ruth Curtain contain many exercises. While writing the second book, Ruth Curtain worked together with Orest Iftime on the solutions to a selected set of exercises from it. After her dead, I continued this project together with Orest.

Control of Distributed Parameter Systems

book project

Since control of systems described by partial differential equations increases in popularity among engineers Yann Le Gorrec and I are working on a book which should support engineers when entering this field. Hence the book should be much less mathematical than the book which I wrote with Ruth Curtain. Early versions of the book have been used for a master course at Eindhoven university of technology. The audience consisted of master students from mechanical and electrical engineering. Based on the experiences we are improving the manuscript.

Finished projects

Book on Infinite-dimensional systems

Since the book with Ruth Curtain is more that 20 years old, we decided to update it. We worked on it for a couple of years and after the death of Ruth in March 2018, I continued with this project. I hope to finish it in 2019.

Based on the book ``An Introduction to Infinite-Dimensional Linear Systems Theory'' some lectures were recorded. They may be found here: Lecture Infinite Dimensional Systems

The order of the videos are: 

  • 1 05 Introduction and Semigroups
  • 1 01 Inputs and Outputs
  • 1 03 Transfer Functions
  • 1 04 Stability and Stabilizability
  • 1 02 Port-Hamiltonian Systems
Scan the QR code or
Download vCard