Welcome to my home page. Here, you can find some information about my professional activities and projects. Please use the tabs above to navigate through the site.
To register for my inaugural lecture, please follow this link.
I am a full professor on Stochastic Processing Interacting Networks at the University of Twente (UT), the director of the Dutch Network on the Mathematics of Operations Research (LNMB), and a Research Fellow of the European research institute EURANDOM.
My research interests centre on stochastic processes on interacting networks. Typical applications I focus on are energy networks, data centres, and high-tech manufacturing. You can find recent publications and project information in the "Research" and "Projects" tabs above.
Next to my research, I am active in promoting gender diversity in academia through my roles as the representative for the Netherlands to the European Women in Mathematics association and to the Committee for Women in Mathematics of the International Mathematical Union. Additionally, I am a member of the advisory boards of the national associations of women in mathematics in Cyprus and in Greece.
Last, I currently serve at the editorial boards of IISE Transactions, Mathematical Methods of Operations Research, OR Spectrum, and INFOR, and have frequently served on the programme committees for conferences in applied probability and operations research.
Links
My CV (updated: March 2025)
My research @UT
arXiv
ORCiD
Research Gate
ResearcherID
Scopus
Energy group @UT
Expertise
Computer Science
- Models
- Approximation (Algorithm)
- Service
- Server
- Distribution Network
Mathematics
- Approximation
- Queue Length
- Asymptotics
Organisations
Ancillary activities
- IISE Transactions (Taylor and Francis Online)Associate editor IISE Transactions
- Mathematical Methods of Operations Research (Springer)Associate editor MMOR
- OR Spectrum (Springer Nature Switzerland AG)Associate editor OR Spectrum
- INFOR: Information Systems and Operational ResearchAssociate editor INFOR
- LNMBDirector LNMB
I focus on the performance of stochastic processing networks with layered architectures with typical application domains on energy networks, data centers, and high-tech manufacturing. In addition, I have worked on perturbation analysis for heavy-tailed risk models, LĂ©vy processes, large deviations for non-monotone stochastic recursions, and proportional fairness in heavy traffic for bandwidth-sharing networks.
Publications
2025
2024
Research profiles
I teach courses in probability, stochastic processes, infectious-disease epidemiology, and performance modelling. I regularly supervise BSc, MSc, and PhD theses, internships, and PDEng projects on these topics. Please contact me for more information on available projects.
I have obtained my University Teaching Qualification diploma (UTQ / BKO) in 2010 and I have continued my training in education through various professional development courses. I have served in the departmental Didactics committee and UTQ committee. I have obtained several grants on research in mathematics education. Find information on my latest project here.
Affiliated study programs
Courses academic year 2024/2025
Courses in the current academic year are added at the moment they are finalised in the Osiris system. Therefore it is possible that the list is not yet complete for the whole academic year.
Courses academic year 2023/2024
Current projects
Stochastic processes driven by non-convex resource allocation problems
The project focuses on stochastic processes of which the dynamics are driven by resource allocation problems related to non-convex optimisation problems. These processes naturally occur as multi-scale models that describe congestion in man-made systems such as energy and communication networks. Being Markov processes on infinite-dimensional state spaces, their analysis is mathematically challenging and current techniques insufficient: Linear approximations of the driving resource allocation problem can lead to a poor understanding of such systems and to suboptimal designs, especially under critical loading. We develop mathematical results in the context of electric vehicle charging, analysing their fluid models and applying them to derive control rules that handle congestion in electricity networks efficiently.
AI for Energy Grids
The project focuses on developing a framework for coordinating flexibility in the distribution grid. Due to the increase of decentralized electricity production and rapid electrification, the distribution grid is becoming ever more unpredictable and overloaded. Grid reinforcements could solve these issues, but in practice this will take too long to solve current day problems. A solution that is usable now is to facilitate flexible use of electricity. Flexibility in this context means to shift the usage of electricity in time where possible, to mitigate overloading. The DSO has a variety of sources of flexibility, such as specific contracts with grid users and flexibility markets. The coordination of these flexibility sources is not trivial, and developing a method to enable this is the focus of this project. This research involves machine learning, mathematical programming, implicit learning, and reinforcement learning. This project is part of the ICAI lab âAI for Energy Gridsâ in the LTP ROBUST programme.
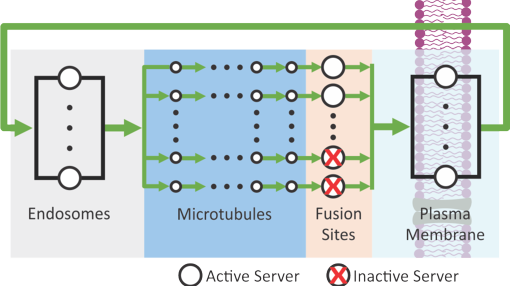
The Mathematics of Stochastic Transport and Signalling in Cells
The aim of this project is to develop stochastic mathematical models for the translocation of key molecular components in cells and the activation of biochemical signalling pathways. Previous mathematical models of cell metabolism have focussed on the macroscale response, using deterministic mean-field algorithms. However, the cell is a crowded environment containing geometrically complicated structures, giving locational specificity to cellular processes. The complexity of a cell means it is biologically unrealistic to consider it a well-mixed compartmental system. This project has three inter-related focus areas: stochastic queuing networks of vesicular trafficking and dynamics in cells, the development of mathematical tools and algorithms for the analysis of transient and steady state behaviour of closed queuing networks, and the development of hybrid mathematical modelling framework for parameter inference and model selection in cellular transport. This project advances understanding of the relative role that different components and processes play in cellular transport and signalling.
Layered stochastic networks with limited resources
This project studies a class of mathematical models that are important in the performance analysis of networks, such as communication, computer, and energy systems. Specifically, the project focuses on the analysis of systems with multiple interacting layers that share limited resources, where the degree of resource sharing is limited by necessity (e.g. a buffer) or by choice (e.g. to guarantee a minimal performance level). These systems are mathematically very challenging, with few known results and insights. We focus on asymptotic and algorithmic techniques for networks where all active servers share a common single resource in a limited processor sharing fashion. We incorporate user impatience and general service times. We prove fluid and diffusion limit theorems of stochastic multi-node networks with multiple interacting layers by using Markov, renewal, and measure-valued processes. On a high level, the methods that we use and develop are from the areas of queueing theory, probability theory, optimization theory, and power systems engineering.
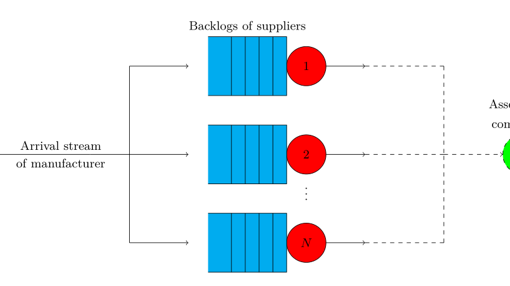
Extreme-Value Theory for Large Fork-Join Queues
The project is inspired by modeling delays in supply chains for high-tech manufacturers, such as ASML, Philips Healthcare, and Boeing. These supply chains are very large compared to the typical supply chain in industry. A common property is that many high-tech suppliers specialize in producing and delivering a specific component of the final product. In this system, the slowest supplier determines the delay of the manufacturer. To model this delay, we consider the N-server fork-join queueing network, in which each server represents a unique supplier, and the arrival stream denotes orders from the manufacturer. We investigate the behavior of the longest queue and the longest waiting time by proving limiting results as the number of servers N converges to infinity. We additionally propose centralized base-stock and capacity policies to minimize costs incurred by delays. To achieve these objectives, we use results from extreme-value theory, diffusion approximations, large deviations principles, theory on heavy-tailed random variables, and newsvendor problems.
In the press
- Wachtrijen in het Wiskundelandschap (in Dutch), Pythagoras 64(3) : 12â15, 2025
- Matematicas en el mundo (in Spanish)
- UPS Smith Prize Winner Reprise
- Feestelijke prijsuitreiking voor gelauwerde wiskundemaster
- We are taking decisions based on bad numbers
- Faces of Women in Mathematics
- Why the amount of queuing time depends on mathematics
- Students gain most from maths-interests balance
- Een snelle knipbeurt of de schoonheid van een vergelijking
News on utwente.nl
Address
University of Twente
Zilverling (building no. 11)
Hallenweg 19
7522 NH Enschede
Netherlands
University of Twente
Zilverling
P.O. Box 217
7500 AE Enschede
Netherlands
Scan the QR code or