About Me
I obtained my PhD at Otto-von-Guericke University Magdeburg. I work on solving techniques for mixed-integer programs (MIPs) on the practical side (branch-and-cut, branch-and-price) as well as polyhedral combinatorics on the theoretical side.
Expertise
Organisations
Publications
UT Research Information System
Affiliated Study Programmes
Master
Courses Academic Year 2023/2024
Courses Academic Year 2022/2023
Current Projects
-
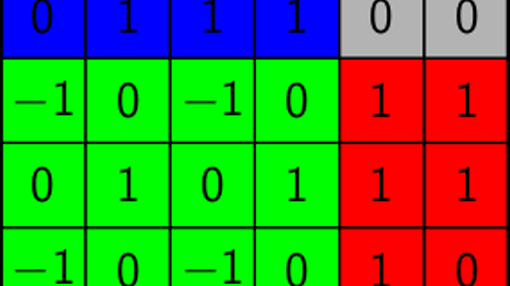
Combinatorial Matrix Recognition
Software Library
A set of tools for recognizing certain combinatorial matrices, such as totally unimodular, balanced, network or series-parallel matrices.
-
Investigating Polyhedra by Oracles
Software Library
Investigating Polyhedra by Oracles (IPO) is a C++ library that enables the analysis of polyhedra that are given implicitly by means of an optimization oracle. The main application is the search for inequalities that are facet-defining for the mixed-integer hull of some mixed-integer optimization problem.
-
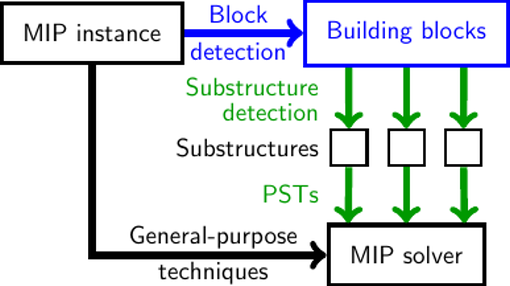
Making Mixed-Integer Programming Solvers Smarter and Faster using Network Matrices
Mixed-integer optimization is a technique to solve complex optimization problems which arise in production planning, logistics and routing. This research will improve the solver software to make it faster. To achieve this, algorithms to find well-known patterns in a given formulation will be developed and tested.
Contact Details
Visiting Address
University of Twente
Faculty of Electrical Engineering, Mathematics and Computer Science
Zilverling
(building no. 11), room 4005
Hallenweg 19
7522NH Enschede
The Netherlands
Mailing Address
University of Twente
Faculty of Electrical Engineering, Mathematics and Computer Science
Zilverling
4005
P.O. Box 217
7500 AE Enschede
The Netherlands